Гравитационный парадокс.
-
depths
- Пользователь
- Сообщения: 1239
- https://www.youtube.com/watch?v=pOfik9PN3Rw
- Зарегистрирован: 30 апр 2015, 22:17
- Репутация: 74
- Настоящее имя: Алексей Лебедев
- Откуда: Екатеринбург
- Контактная информация:
Re: Гравитационный парадокс.
Как получаются ряды с членами из одного слоя всем понятно?
Таким образом имеем для одного слоя:
1/(r[sub]n[/sub][sup]m[/sup])^2
где n -это номер слоя (1, 2, 3 и т.д.), m -количество свободных рядов для этого слоя (пробовал найти закономерность для этой переменной, не получилось), нумерует от центра к периферии.
Будет выполняться неравенство: r[sub]n[/sub][sup]1[/sup] < r[sub]n[/sub][sup]2[/sup] и
r[sub]n+1[/sub][sup]m[/sup] > r[sub]n[/sub][sup]m[/sup]
Чтобы легче было анализировать сходимость/расходимость силы от суммы всех рядов можно r[sub]n[/sub][sup]m[/sup] заменить на r[sub]n[/sub][sup]1[/sup] или на r[sub]0[/sub]*к[sub]n[/sub]
Таким образом имеем для одного слоя:
1/(r[sub]n[/sub][sup]m[/sup])^2
где n -это номер слоя (1, 2, 3 и т.д.), m -количество свободных рядов для этого слоя (пробовал найти закономерность для этой переменной, не получилось), нумерует от центра к периферии.
Будет выполняться неравенство: r[sub]n[/sub][sup]1[/sup] < r[sub]n[/sub][sup]2[/sup] и
r[sub]n+1[/sub][sup]m[/sup] > r[sub]n[/sub][sup]m[/sup]
Чтобы легче было анализировать сходимость/расходимость силы от суммы всех рядов можно r[sub]n[/sub][sup]m[/sup] заменить на r[sub]n[/sub][sup]1[/sup] или на r[sub]0[/sub]*к[sub]n[/sub]
Re: Гравитационный парадокс.
depths писал(а):Таким образом имеем для одного слоя:
1/(r[sub]n[/sub][sup]m[/sup])^2
где n -это номер слоя (1, 2, 3 и т.д.),
Если всё это для одного слоя, то зачем тут номер слоя?
Не понял вообще для чего r возводить в степень m.
Или это не степень?
Запись непонятная.
depths писал(а):m -количество свободных рядов для этого слоя (пробовал найти закономерность для этой переменной, не получилось), нумерует от центра к периферии.
Что такое количество свободных рядов для слоя?
Что такое вообще свободный ряд?
depths писал(а):Будет выполняться неравенство: r[sub]n[/sub][sup]1[/sup] < r[sub]n[/sub][sup]2[/sup] и
r[sub]n+1[/sub][sup]m[/sup] > r[sub]n[/sub][sup]m[/sup]
Чтобы легче было анализировать сходимость/расходимость силы от суммы всех рядов можно r[sub]n[/sub][sup]m[/sup] заменить на r[sub]n[/sub][sup]1[/sup] или на r[sub]0[/sub]*к[sub]n[/sub]
Здесь тоже. m - это степень или что?
---------
А вообще.
Кроме моего замечания по поводу r не забудьте умножать на косинус, чтобы вычислить проекцию силы на ось.
Вы эти углы упаритесь вычислять.
И без упрощения вашей модели никак не обойтись.
Непонятно, зачем вы выбрали такую сложную модель.
Есть гораздо проще.
Могу предложить.
Только что это вам даст?
Вот вдруг сойдется ряд для одного слоя.
Что дальше?
Просто добавлять слои не получится при выбранном расположении тел.
------------------------
Вот способ проще.
Берем только один слой.
Массы в каждом ряду меняются так:
1 шаг - 2 шара.
2 шаг - 3 шара.
3 шаг - 4 шара.
...
n шаг - (n+1) шара.
Далее делаем упрощение (как и в случае пирамидки. См. выше).
Сдвигаем все шары в каждом ряду в ребро.
Такое упрощение работает в сторону уменьшения силы. Как и в случае пирамидки. См. выше.
Принимаем r = 1. m = 1 (m - масса каждого шарика).
Вычисляем силу от каждого ряда шаров и умножаем её на косинус альфа (чтобы получить проекцию на центральную ось).
Выносим все константы за скобки и получаем ряд:
(n+1)/n^2
-
depths
- Пользователь
- Сообщения: 1239
- Зарегистрирован: 30 апр 2015, 22:17
- Репутация: 74
- Настоящее имя: Алексей Лебедев
- Откуда: Екатеринбург
- Контактная информация:
Re: Гравитационный парадокс.
Insider писал(а):Если всё это для одного слоя, то зачем тут номер слоя?
Не понял вообще для чего r возводить в степень m.
Или это не степень?
Запись непонятная.
Это не степень.
m это индекс, я его так записал, сверху. Если не удобно можно так r[sub]nm[/sub]
Слой - это горизонтальный ряд шаров, рассматриваю левую (половину) часть пирамиды шаров (кругов) на плоскости (грань обычной пирамиды).
Insider писал(а):Что такое количество свободных рядов для слоя?
Что такое вообще свободный ряд?
Проведем лучь от верхнего шара через свободный шар в третьем слое (использую слово слой та как слово ряд занято под понятие бесконечный ряд). Почему свободный, из-за того что два других уже заняты - вертикальная ось и ребро.
На луче через равные промежутки будут лежать шары. Кождый шар также лежит в каком-нибудь слое. В каком? В слое с номером кратным трём.
Последний раз редактировалось depths 01 июл 2017, 07:23, всего редактировалось 1 раз.
-
depths
- Пользователь
- Сообщения: 1239
- Зарегистрирован: 30 апр 2015, 22:17
- Репутация: 74
- Настоящее имя: Алексей Лебедев
- Откуда: Екатеринбург
- Контактная информация:
Re: Гравитационный парадокс.
Я ранее писал, что число шаров в слое равно номеру слоя. Тут у меня ошибка, не равно.
-
Александр
- Администратор
- Сообщения: 983
- Зарегистрирован: 30 апр 2015, 20:00
- Репутация: 174
- Откуда: Спб
Re: Гравитационный парадокс.
Insider писал(а):Всё, что положено, делается. По ссылке есть подробное описание модели.
Берем каждый шарик и вычисляем силу от него, суммируем. Всё.
Что конкретно не понятно?
Просто хочу заметить что предложенный вами метод не предполагает вычисления БГП, а лишь даёт возможность ответить на вопрос будет ли сила бесконечная или конечна? Я правильно понимаю?
[spoil][/spoil]
Если представить поле из шариков на плоскости, ты вы считает все силы по отношению к 1,1 шарику, 1,2 и т.д.?
Камни с неба падать не могут, им там неоткуда взяться! (Парижская Академия Наук о метеоритах, 1772 г)
Правила форума
Правила форума
-
Александр
- Администратор
- Сообщения: 983
- Зарегистрирован: 30 апр 2015, 20:00
- Репутация: 174
- Откуда: Спб
Re: Гравитационный парадокс.
Гравитационная проблема N- тела
Галактики контролируются силой тяжести, которая действует между всеми телами,за исключением самовзаимодействия. Во-первых, мы рассмотрим прямое применение закона тяжести Ньютона, а затем в сложном иерархическом приближении.
Гравитационное взаимодействие между всеми парами тел (кроме самовзаимодействия) введет сумму в правую часть уравнения (4.2) и станет
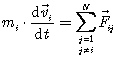 ( 4.3)
( 4.3)
Сила,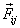 данная универсальным законом гравитации Ньютона, дается формулой
данная универсальным законом гравитации Ньютона, дается формулой
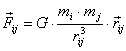 ( 4.4)
( 4.4)
где G - гравитационная постоянная Ньютона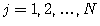 ,
, 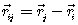 и
и 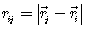
После затыкания члена для скорости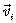 (уравнение 4.1) в левую часть уравнения (4.2), уравнение 4.4 упрощается до формы, где ускорение
(уравнение 4.1) в левую часть уравнения (4.2), уравнение 4.4 упрощается до формы, где ускорение 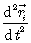 не зависит от массы выбранного тела i
не зависит от массы выбранного тела i
 ( 4.5)
( 4.5)
Поэтому для изучения этой проблемы необходим численный подход. и т.д.
https://kof.zcu.cz/st/dis/schwarzmeier/ ... tml#_ftn35
Галактики контролируются силой тяжести, которая действует между всеми телами,за исключением самовзаимодействия. Во-первых, мы рассмотрим прямое применение закона тяжести Ньютона, а затем в сложном иерархическом приближении.
Гравитационное взаимодействие между всеми парами тел (кроме самовзаимодействия) введет сумму в правую часть уравнения (4.2) и станет
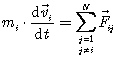 ( 4.3)
( 4.3)Сила,
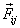 данная универсальным законом гравитации Ньютона, дается формулой
данная универсальным законом гравитации Ньютона, дается формулой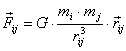 ( 4.4)
( 4.4)где G - гравитационная постоянная Ньютона
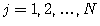 ,
, 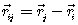 и
и 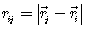
После затыкания члена для скорости
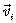 (уравнение 4.1) в левую часть уравнения (4.2), уравнение 4.4 упрощается до формы, где ускорение
(уравнение 4.1) в левую часть уравнения (4.2), уравнение 4.4 упрощается до формы, где ускорение 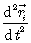 не зависит от массы выбранного тела i
не зависит от массы выбранного тела i ( 4.5)
( 4.5)Поэтому для изучения этой проблемы необходим численный подход. и т.д.
https://kof.zcu.cz/st/dis/schwarzmeier/ ... tml#_ftn35
Камни с неба падать не могут, им там неоткуда взяться! (Парижская Академия Наук о метеоритах, 1772 г)
Правила форума
Правила форума
-
Александр
- Администратор
- Сообщения: 983
- Зарегистрирован: 30 апр 2015, 20:00
- Репутация: 174
- Откуда: Спб
Re: Гравитационный парадокс.
Динамическая системы, состоящей из N тел под действием силы тяжести, не разрешима для для более чем двух тел
https://kof.zcu.cz/ вот сайт кафедры физик где провели моделирование которое и касается нашей темы.
Кстати там есть исходники на C.
вот перевод
В физике средней школы нас учит тому, что сила тяжести - это сила, действующая удаленно и мгновенно между всеми телами, как было указано сэром Исааком Ньютоном , основанным на его наблюдениях за природой и рассуждениями. Согласно теории Ньютона «каждая частица материи во вселенной притягивает каждую другую частицу силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрату их расстояний».
В математическом описании гравитации мы начнем с поля скалярного поля тяготения, а не поля векторной силы. Предположим, что мы имеем некоторое расположение точек массы, зафиксированных в пространстве, и нас интересует их кумулятивный эффект на некоторую данную точку пространства. Общий гравитационный потенциал N тел с массами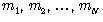 в некоторой точке пространства аддитивен и определяется суммой всех потенциалов от отдельных тел
в некоторой точке пространства аддитивен и определяется суммой всех потенциалов от отдельных тел 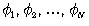 на расстояниях
на расстояниях 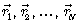 от данной точки в пространстве, так как [align=center]
от данной точки в пространстве, так как [align=center] ( 5.5)[/align]
( 5.5)[/align]
Конфигурация N точечных масс (система N- тел) может быть обобщена на непрерывную функцию распределения плотности массы p , которая является функцией положения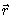 Если мы будем писать
Если мы будем писать 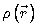 как функцию координат,
как функцию координат, 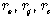 то
то 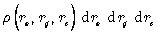 это масса, содержащаяся в небольшом ящике объема
это масса, содержащаяся в небольшом ящике объема 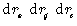 расположенном в точке
расположенном в точке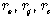 Плотность масс
Плотность масс 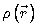 в определенном месте определяется суммой источников массы (точечных масс) в бесконечно малом элементе объема. Функция распределения плотности массы
в определенном месте определяется суммой источников массы (точечных масс) в бесконечно малом элементе объема. Функция распределения плотности массы 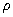 представляет собой функцию, описывающую распределение вещества (звезд) в системе (галактике). Переход от дискретной к
представляет собой функцию, описывающую распределение вещества (звезд) в системе (галактике). Переход от дискретной к
непрерывной форме может быть приблизительно выражен как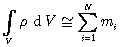
Аналогичным образом гравитационный потенциал, создаваемый непрерывным распределением массы вместо отдельных тел в качестве источников потенциала, может быть выражен непрерывно. Суммирование (5.5) превращается в интеграцию в местах (макроскопически), непрерывно заполненных веществом.
Градиентом потенциала является гравитационная сила, действующая на тело с единичной массой, кроме знака минус.
"От себя: - опять знак минус" он правильный только его не как не объясняют.
Исследовательский корпус единичной массы будет испытывать в любой точке, заданной позиционной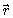 силой,
силой,
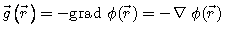 (5.6)
(5.6)
Эта величина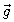 называется интенсивностью гравитационного поля.
называется интенсивностью гравитационного поля.
С непрерывными функциями мы можем использовать уравнение Пуассона (Greiner, 2004)
 (5.7)
(5.7)
Здесь мы получаем связь между гравитационным потенциалом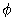 и массой
и массой 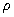 Уравнение Пуассона служит одним из основных управляющих уравнений в нашем исследовании устойчивости, структуры и динамики самогравитирующих систем. Массовая плотность, необходимая для генерации потенциала, может быть найдена путем решения уравнения Пуассона. С другой стороны, из известной плотности массы мы можем определить гравитационный потенциал через уравнение Пуассона.
Уравнение Пуассона служит одним из основных управляющих уравнений в нашем исследовании устойчивости, структуры и динамики самогравитирующих систем. Массовая плотность, необходимая для генерации потенциала, может быть найдена путем решения уравнения Пуассона. С другой стороны, из известной плотности массы мы можем определить гравитационный потенциал через уравнение Пуассона.
Различные компоненты галактик (диск, выпуклость ... и гало) имеют собственную функцию плотности массы в глобальном гравитационном потенциале. Уравнение Пуассона дает нам связь между ними. Для модели самогравитации мы должны найти глобальный гравитационный потенциал, в котором плотность масс всех частей галактики объединяется как
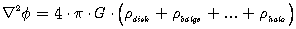 (5.8)
(5.8)
И так далее https://kof.zcu.cz/st/dis/schwarzmeier/ ... odels.html
Темная материя
Предполагается, что невидимая материя обеспечивает эту пропущенную гравитацию. Ян Х. Оорт (1932), изучавший движение звезд в галактике Млечный Путь, был первым, кто заметил, что какая-то материя в нашей галактике «отсутствует». Плоские кривые вращения спиральных галактик на большом галактоцентрическом расстоянии предполагают, что ореол невидимой материи может существовать вокруг спиральных галактик; этот темный ореол может продолжать вносить свой вклад в очень большие радиусы. Фриц Цвикки [50] изучал движение галактик в скоплении скоплений комы галактик в 1933 году. Он обнаружил, что скорости галактик настолько велики, что они давно должны вылететь из кластера галактик. Поскольку в кластере нет признаков разлета, отдельные силы невидимого источника должны удерживать его вместе. Как правило, предполагается, что какое-то дополнительное вещество, невидимое для нас, должно гравитационно связать эти галактики (Zwicky, 1937).
От себя: в модель приходится вводить темную энергия, что бы рукава галактик не разлетелись. Масса этой темной материи 30% от всей массы галактики.
https://kof.zcu.cz/ вот сайт кафедры физик где провели моделирование которое и касается нашей темы.
Кстати там есть исходники на C.
вот перевод
В физике средней школы нас учит тому, что сила тяжести - это сила, действующая удаленно и мгновенно между всеми телами, как было указано сэром Исааком Ньютоном , основанным на его наблюдениях за природой и рассуждениями. Согласно теории Ньютона «каждая частица материи во вселенной притягивает каждую другую частицу силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрату их расстояний».
В математическом описании гравитации мы начнем с поля скалярного поля тяготения, а не поля векторной силы. Предположим, что мы имеем некоторое расположение точек массы, зафиксированных в пространстве, и нас интересует их кумулятивный эффект на некоторую данную точку пространства. Общий гравитационный потенциал N тел с массами
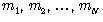 в некоторой точке пространства аддитивен и определяется суммой всех потенциалов от отдельных тел
в некоторой точке пространства аддитивен и определяется суммой всех потенциалов от отдельных тел 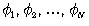 на расстояниях
на расстояниях 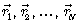 от данной точки в пространстве, так как [align=center]
от данной точки в пространстве, так как [align=center] ( 5.5)[/align]
( 5.5)[/align]Конфигурация N точечных масс (система N- тел) может быть обобщена на непрерывную функцию распределения плотности массы p , которая является функцией положения
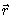 Если мы будем писать
Если мы будем писать 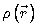 как функцию координат,
как функцию координат, 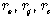 то
то 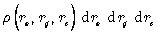 это масса, содержащаяся в небольшом ящике объема
это масса, содержащаяся в небольшом ящике объема 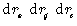 расположенном в точке
расположенном в точке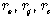 Плотность масс
Плотность масс 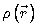 в определенном месте определяется суммой источников массы (точечных масс) в бесконечно малом элементе объема. Функция распределения плотности массы
в определенном месте определяется суммой источников массы (точечных масс) в бесконечно малом элементе объема. Функция распределения плотности массы 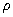 представляет собой функцию, описывающую распределение вещества (звезд) в системе (галактике). Переход от дискретной к
представляет собой функцию, описывающую распределение вещества (звезд) в системе (галактике). Переход от дискретной к непрерывной форме может быть приблизительно выражен как
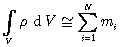
Аналогичным образом гравитационный потенциал, создаваемый непрерывным распределением массы вместо отдельных тел в качестве источников потенциала, может быть выражен непрерывно. Суммирование (5.5) превращается в интеграцию в местах (макроскопически), непрерывно заполненных веществом.
Градиентом потенциала является гравитационная сила, действующая на тело с единичной массой, кроме знака минус.
"От себя: - опять знак минус" он правильный только его не как не объясняют.
Исследовательский корпус единичной массы будет испытывать в любой точке, заданной позиционной
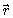 силой,
силой, 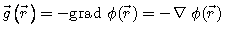 (5.6)
(5.6)Эта величина
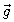 называется интенсивностью гравитационного поля.
называется интенсивностью гравитационного поля.С непрерывными функциями мы можем использовать уравнение Пуассона (Greiner, 2004)
 (5.7)
(5.7)Здесь мы получаем связь между гравитационным потенциалом
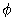 и массой
и массой 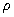 Уравнение Пуассона служит одним из основных управляющих уравнений в нашем исследовании устойчивости, структуры и динамики самогравитирующих систем. Массовая плотность, необходимая для генерации потенциала, может быть найдена путем решения уравнения Пуассона. С другой стороны, из известной плотности массы мы можем определить гравитационный потенциал через уравнение Пуассона.
Уравнение Пуассона служит одним из основных управляющих уравнений в нашем исследовании устойчивости, структуры и динамики самогравитирующих систем. Массовая плотность, необходимая для генерации потенциала, может быть найдена путем решения уравнения Пуассона. С другой стороны, из известной плотности массы мы можем определить гравитационный потенциал через уравнение Пуассона.Различные компоненты галактик (диск, выпуклость ... и гало) имеют собственную функцию плотности массы в глобальном гравитационном потенциале. Уравнение Пуассона дает нам связь между ними. Для модели самогравитации мы должны найти глобальный гравитационный потенциал, в котором плотность масс всех частей галактики объединяется как
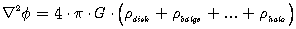 (5.8)
(5.8)И так далее https://kof.zcu.cz/st/dis/schwarzmeier/ ... odels.html
Темная материя
Предполагается, что невидимая материя обеспечивает эту пропущенную гравитацию. Ян Х. Оорт (1932), изучавший движение звезд в галактике Млечный Путь, был первым, кто заметил, что какая-то материя в нашей галактике «отсутствует». Плоские кривые вращения спиральных галактик на большом галактоцентрическом расстоянии предполагают, что ореол невидимой материи может существовать вокруг спиральных галактик; этот темный ореол может продолжать вносить свой вклад в очень большие радиусы. Фриц Цвикки [50] изучал движение галактик в скоплении скоплений комы галактик в 1933 году. Он обнаружил, что скорости галактик настолько велики, что они давно должны вылететь из кластера галактик. Поскольку в кластере нет признаков разлета, отдельные силы невидимого источника должны удерживать его вместе. Как правило, предполагается, что какое-то дополнительное вещество, невидимое для нас, должно гравитационно связать эти галактики (Zwicky, 1937).
От себя: в модель приходится вводить темную энергия, что бы рукава галактик не разлетелись. Масса этой темной материи 30% от всей массы галактики.
Камни с неба падать не могут, им там неоткуда взяться! (Парижская Академия Наук о метеоритах, 1772 г)
Правила форума
Правила форума
Re: Гравитационный парадокс.
Александр писал(а):Просто хочу заметить что предложенный вами метод не предполагает вычисления БГП, а лишь даёт возможность ответить на вопрос будет ли сила бесконечная или конечна? Я правильно понимаю?
Правильно. Только если сила бесконечна, то ни о каком подсчете не может быть и речи.
Александр писал(а):Если представить поле из шариков на плоскости, ты вы считает все силы по отношению к 1,1 шарику, 1,2 и т.д.?
Не понял вопроса. Почему мы должны представлять поле в виде шариков на плоскости?
Я считаю силы от всех шариков по отношения только к одному шарику (расчетному телу).
Re: Гравитационный парадокс.
Александр писал(а):Гравитационная проблема N- тела
Что вы хотите сказать этими постами?
Эта проблема для динамики тел (расчета последующих положений тел).
Мы рассчитываем статику, то есть, просто действие сил на расчетное тело.
Вот есть тело. На него уже сейчас действуют все силы от всех тел Вселенной (по Катющику).
Это и есть БГП. Его и оцениваем.
-
Александр
- Администратор
- Сообщения: 983
- Зарегистрирован: 30 апр 2015, 20:00
- Репутация: 174
- Откуда: Спб
Re: Гравитационный парадокс.
Insider писал(а):Что вы хотите сказать этими постами?
Я хочу сказать, что и ваш и наш математический и другой анализ мягко сказать наивны.
Я пальцем в небо хочу угадать значение БГП по звездам. А Вы на основание наивной модели шариков доказываете что суперпозиции полей нет. Она есть и это очевидно.
И все наши споры видеться мне как на ярмарка тщеславия. Все делают вид что знают, а капни по глубже...
Казалась бы серьезный институт, проделана хорошая работа и вот рукава у галактик разлетаются и что бы это как то объяснить нужно водить черную энергия. Катющик к слову, нас тоже не окатил объяснениями, но 99% делают вид что всё понимают. Мне лично устал спорить. Хочу развития, а не отстаивать какую то из точек зрения.
Insider писал(а):Эта проблема для динамики тел (расчета последующих положений тел).
нет. посмотри ещё раз формулу там нет скоростей. там только вектор силы.
Камни с неба падать не могут, им там неоткуда взяться! (Парижская Академия Наук о метеоритах, 1772 г)
Правила форума
Правила форума
Re: Гравитационный парадокс.
Александр писал(а):А Вы на основание наивной модели шариков доказываете что суперпозиции полей нет. Она есть и это очевидно.
При чем тут "суперпозиций нет"???!!!
Как это нет суперпозиции, если я считаю силу от каждого шарика Вселенной!!!???
Кошмар! Вы вообще о чем?!
Похоже, вы вообще ничего не поняли.
Короче, будет желание разобраться, пишите.
Александр писал(а):нет. посмотри ещё раз формулу там нет скоростей. там только вектор силы.
Там есть всё, что нужно! Подробнее сами разбирайтесь.
https://ru.wikipedia.org/wiki/%D0%93%D1 ... 0%B5%D0%BB
Эта задача никак не относится к тому, что я делаю для анализа БГП.
Александр писал(а):А Вы на основание наивной модели шариков
Эта модель на основе утверждений Катющика о БГП.
А именно, что на тело действуют силы от всех масс бесконечной и однородной Вселенной.
И при таком подходе данная модель никакая не наивная, а вполне состоятельная.
Александр писал(а):И все наши споры видеться мне как на ярмарка тщеславия.
Это вам так видится. И я с вами не спорю.
Re: Гравитационный парадокс.
Александр писал(а): Хочу развития, а не отстаивать какую то из точек зрения.
Замечательно. Что же вам мешает взять букварь по физике и развиваться? Для начала можно взять многотомник Фейнмана.
- Rusfermer
- Посторонний
- Сообщения: 961
- Зарегистрирован: 18 сен 2018, 22:36
- Репутация: 0
- Настоящее имя: Алексей Веселов
- Откуда: Питер
Re: Гравитационный парадокс.
Блин! Почему самые интересные темы находятся [s]в какой то жо...[/s] на задворках форума!? Нормальные учёные их бы в шапку вынесли! А здесь? Ньюфизики бл..! Позорище!
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей и 5 гостей
